RMDNSTSW | Zi-US - Quantum Finance Risk Model

Overview

The Quantum Finance Risk Model (QFRM) is a cutting-edge financial risk analysis tool that combines quantum computing simulations with traditional risk metrics to provide comprehensive portfolio risk assessment.

Key Features

Real-time market data from Yahoo Finance (19 assets across stocks, indices, commodities, crypto)
20-qubit quantum circuit for risk state analysis using IBM Qiskit
Traditional metrics: VaR, CVaR, Sharpe Ratio, Maximum Drawdown, Volatility
4-second dynamic 3D/2D quantum risk simulations
Cross-asset correlation matrices with entropy calculations
Comprehensive JSON, PNG, HTML, GIF, and TXT output formats

Latest Results

-2.68%

VaR (95%)

-4.29%

CVaR (95%)

29.35%

Volatility

1.15

Sharpe Ratio

0.146

Quantum Risk

331

Quantum States

Installation

Clone the repository and install dependencies to get started with QFRM.

Quick Install

# Clone the repository
git clone https://github.com/shellworlds/RMDNSTSW.git
cd RMDNSTSW

# Install dependencies
pip install -r requirements.txt

# Run the model
python qfrm.py

Requirements

Package	Version	Purpose
qiskit	≥1.0.0	Quantum circuit simulation
qiskit-aer	≥0.13.0	Aer quantum simulator backend
yfinance	≥0.2.28	Yahoo Finance market data
numpy	≥1.24.0	Numerical computations
matplotlib	≥3.7.0	Static & dynamic visualizations
plotly	≥5.14.0	Interactive HTML reports

Quick Start

RUN python qfrm.py [options]

Execute the quantum finance risk model with customizable parameters.

Command Line Options

Option	Type	Default	Description
--qubits	int	20	Number of qubits in quantum circuit
--shots	int	5000	Number of quantum measurement shots
--output	string	./finance_risk_output	Output directory for reports

Example Commands

# Default execution (20 qubits, 5000 shots)
python qfrm.py

# Quick test with reduced parameters
python qfrm.py --qubits 10 --shots 1000

# High precision simulation
python qfrm.py --qubits 25 --shots 10000 --output ./high_precision

Expected Output

================================================================================
QUANTUM FINANCE RISK MODEL - EXECUTION COMPLETE
================================================================================
Generated Output Files:
  📊 Dashboard PNG: ./RMDNSTSW/finance_risk_output/finance_risk_dashboard_*.png
  📈 Interactive HTML: ./RMDNSTSW/finance_risk_output/finance_risk_report_*.html
  📋 JSON Report: ./RMDNSTSW/finance_risk_output/finance_risk_report_*.json
  📝 Text Summary: ./RMDNSTSW/finance_risk_output/risk_summary_*.txt
  🎬 Simulation GIF: ./RMDNSTSW/finance_risk_output/quantum_risk_simulation_*.gif
  🎬 Evolution GIF: ./RMDNSTSW/finance_risk_output/risk_evolution_*.gif
================================================================================

Dynamic Simulations

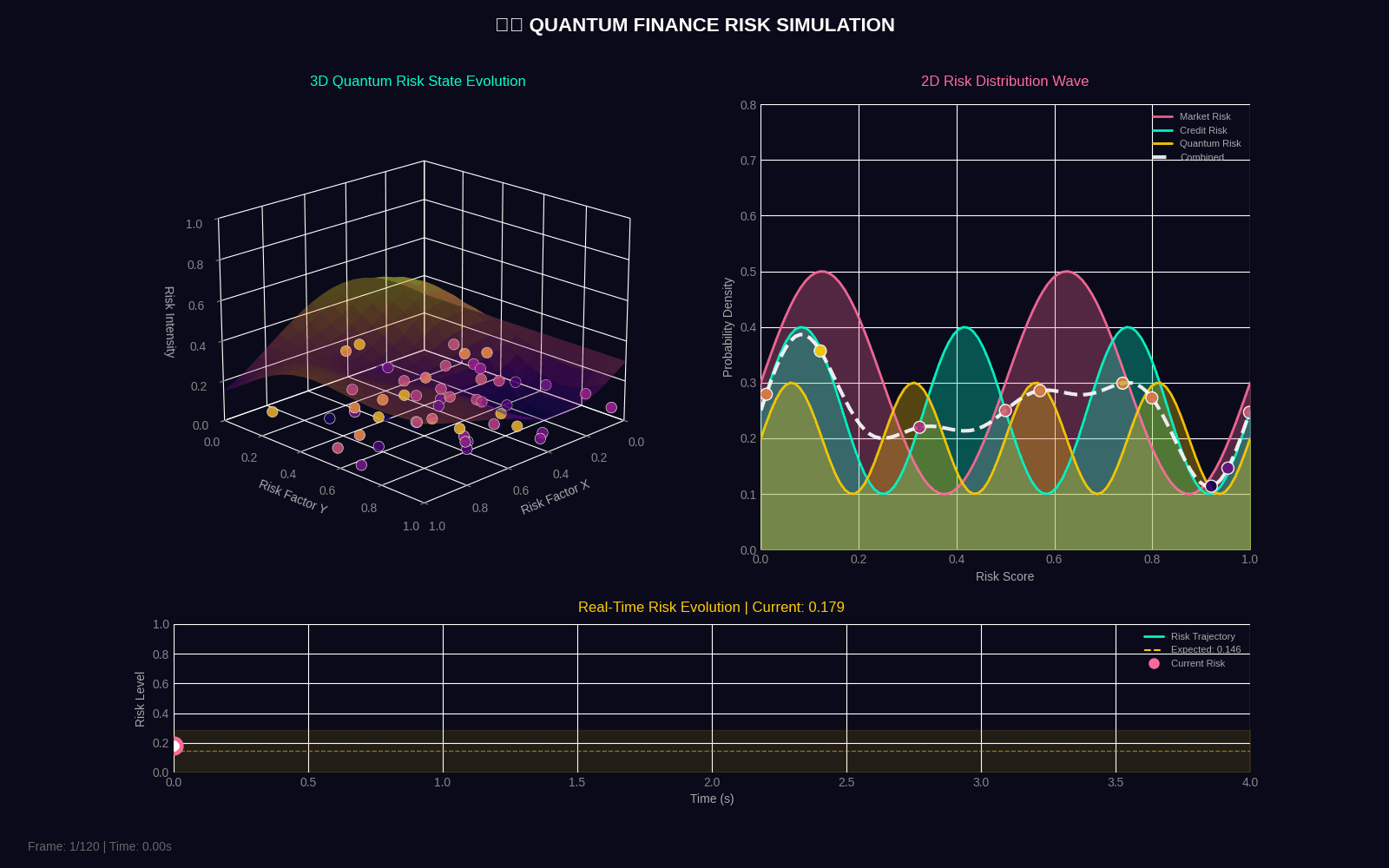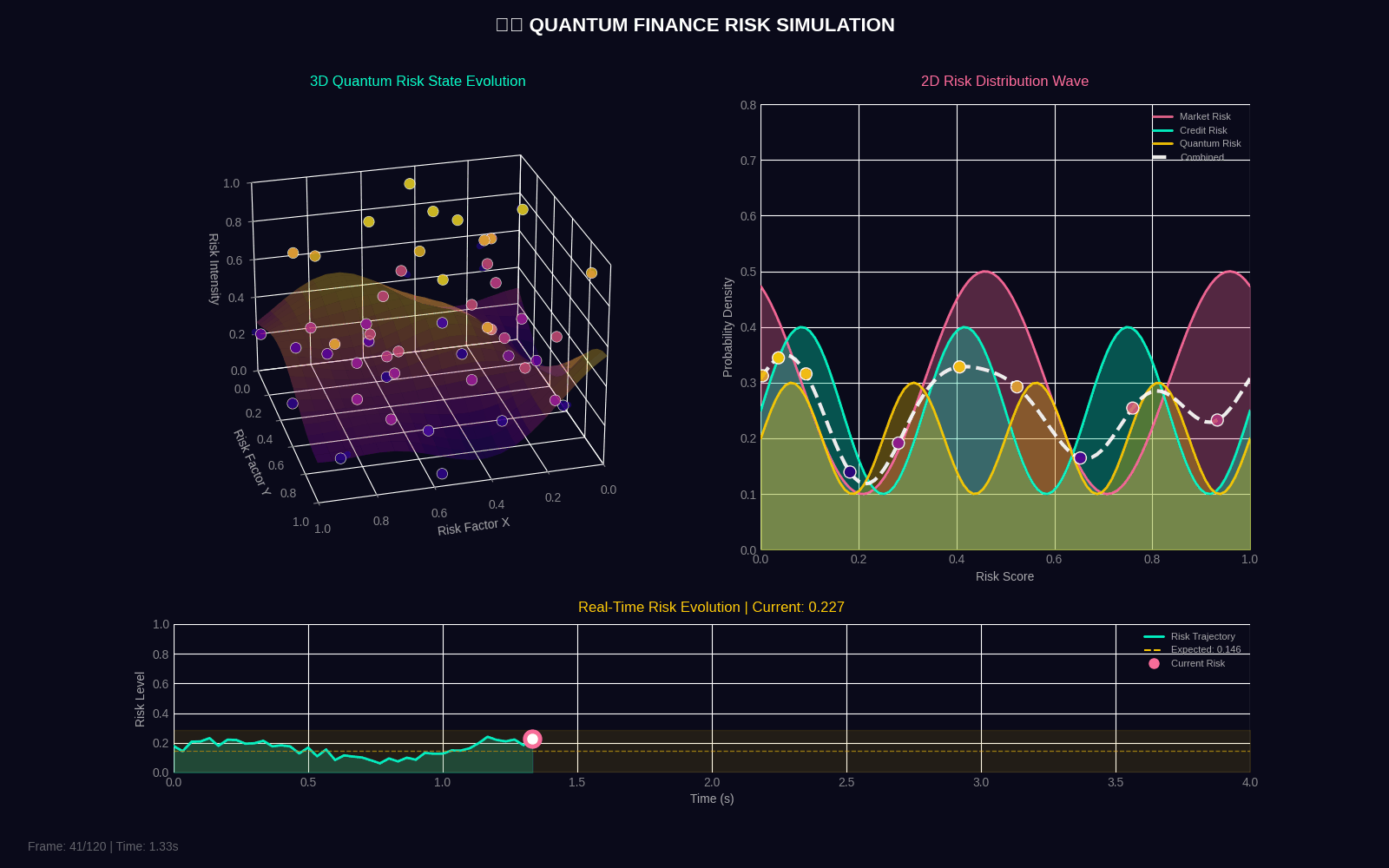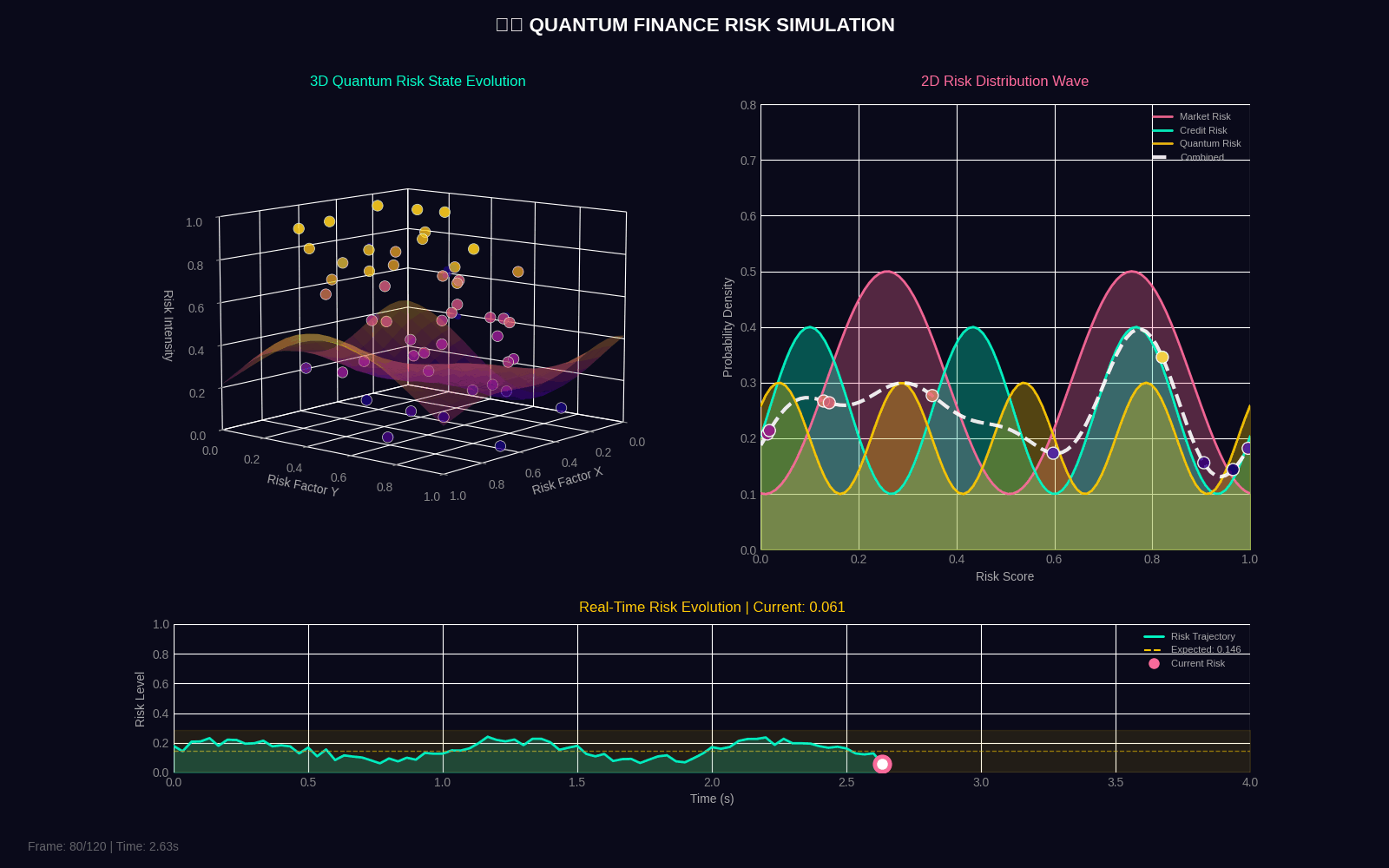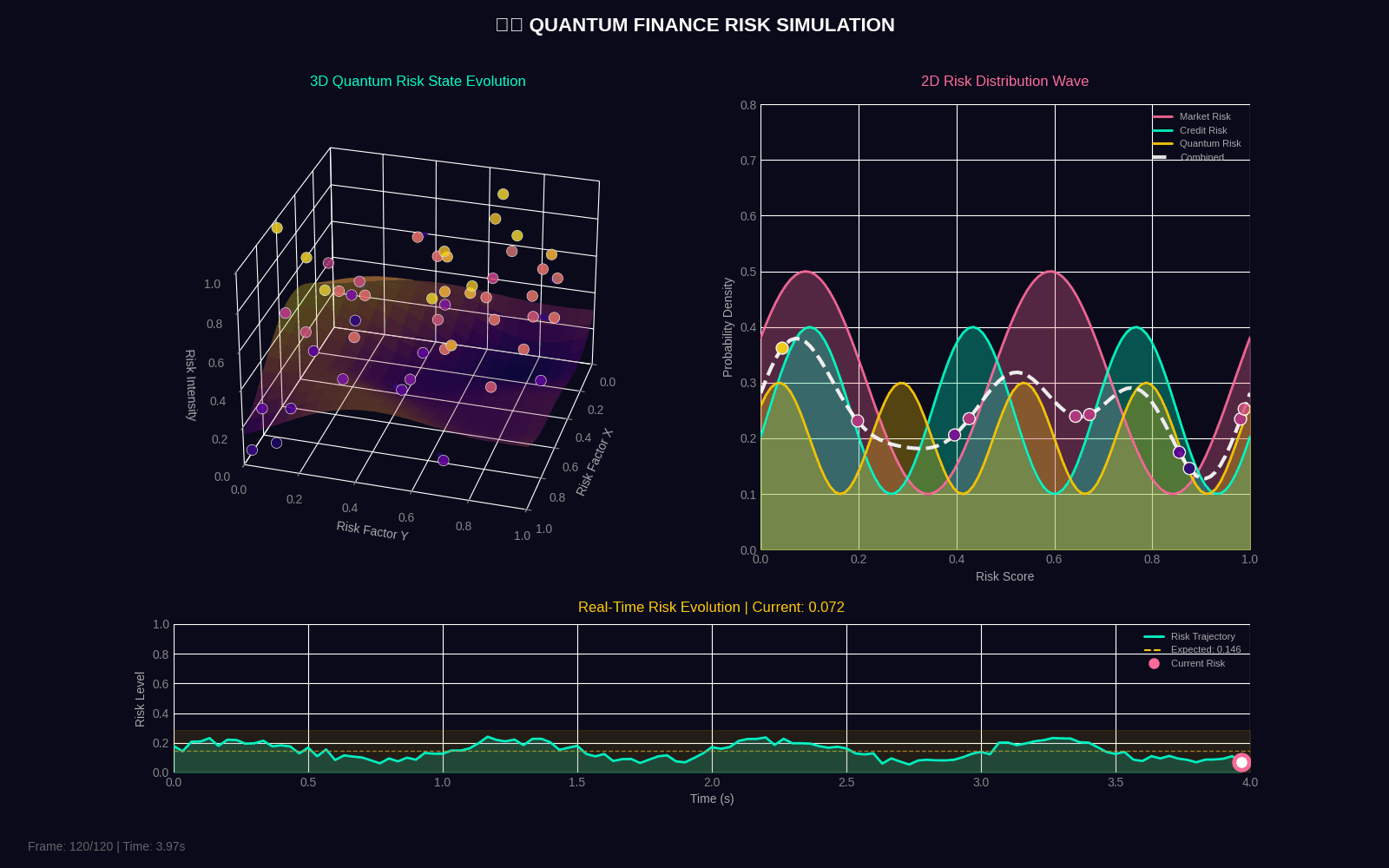
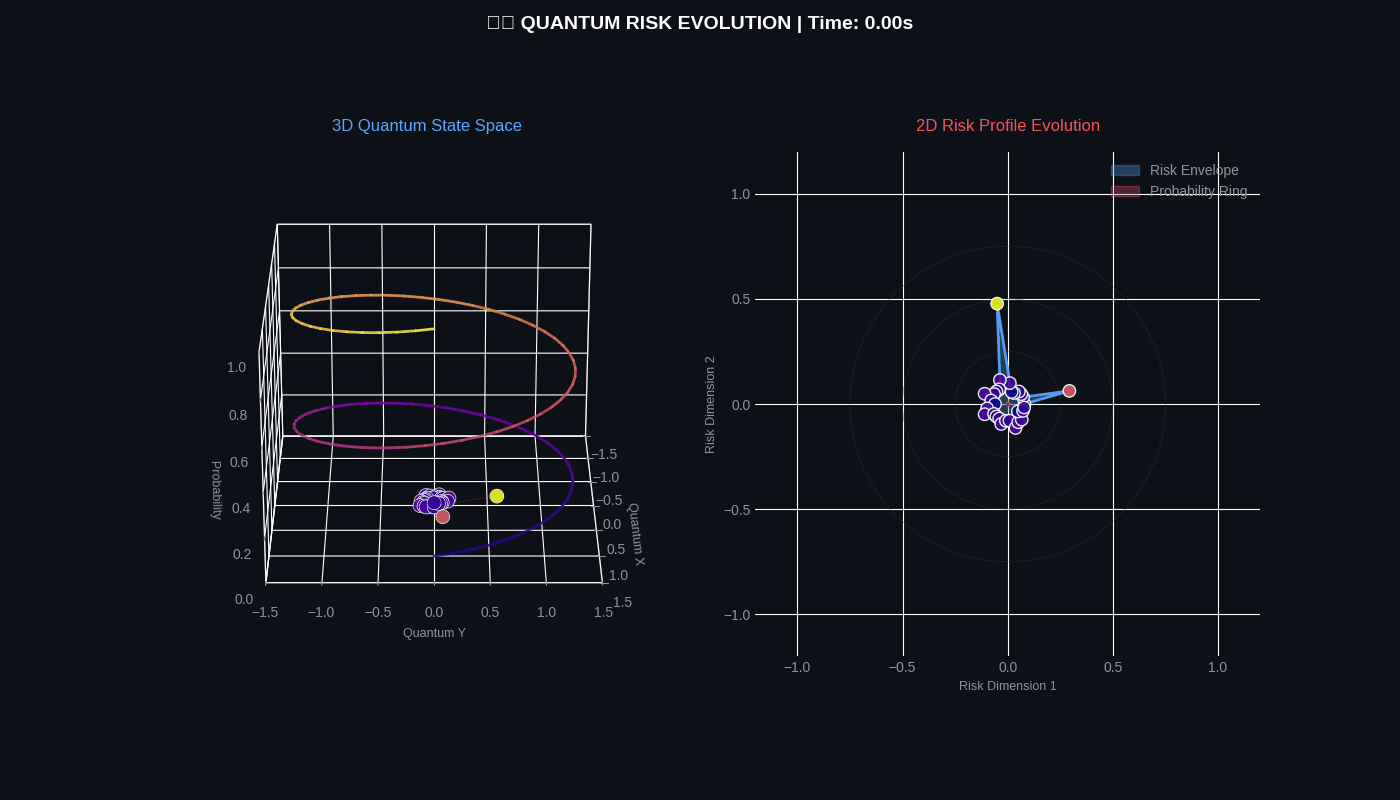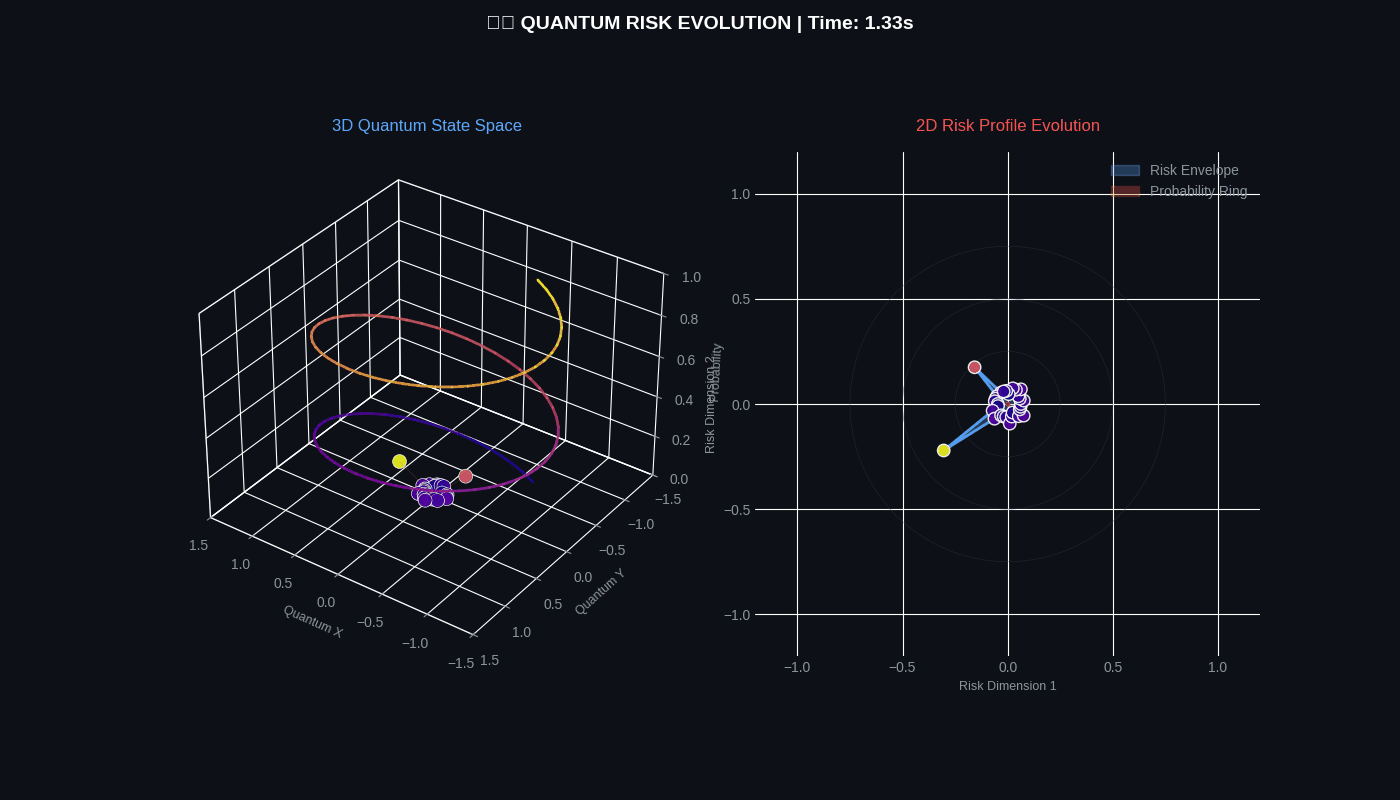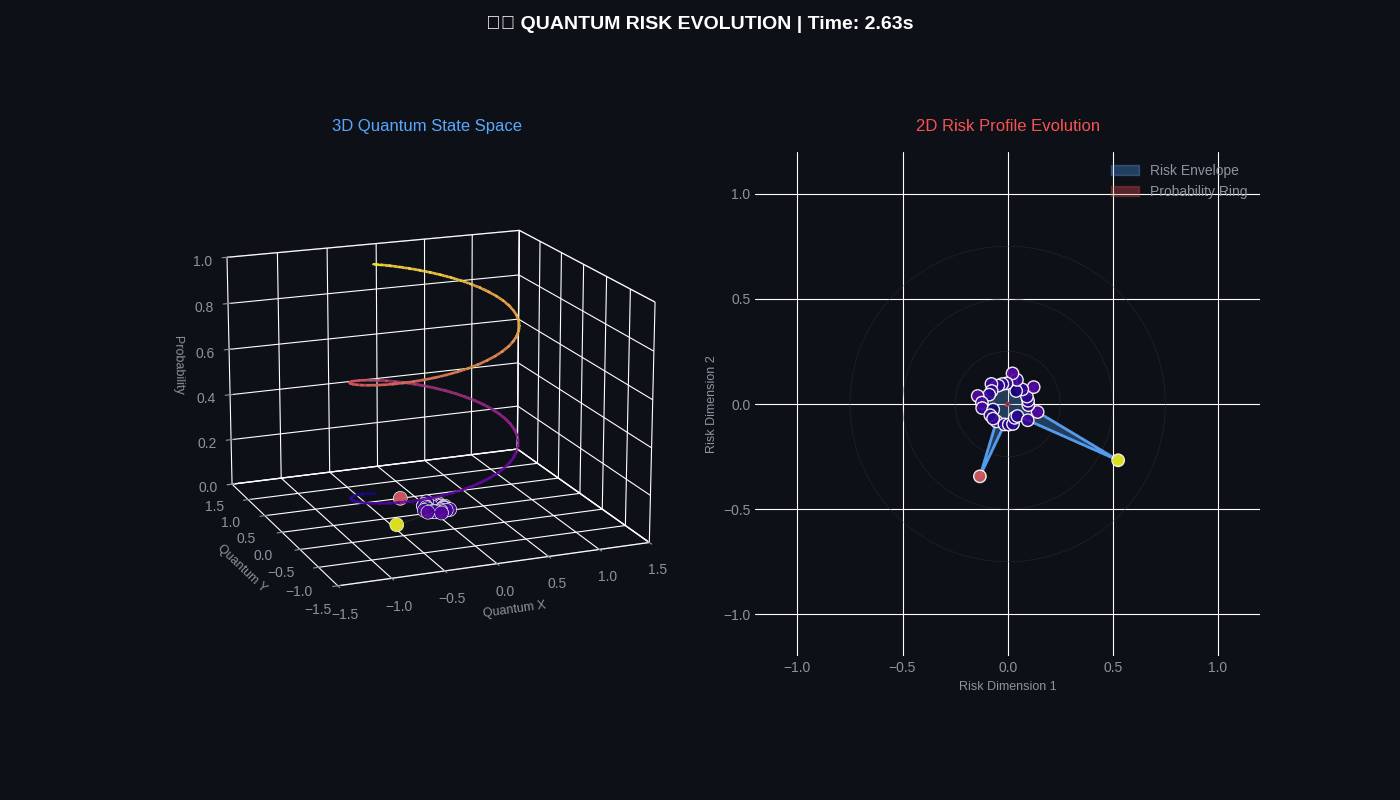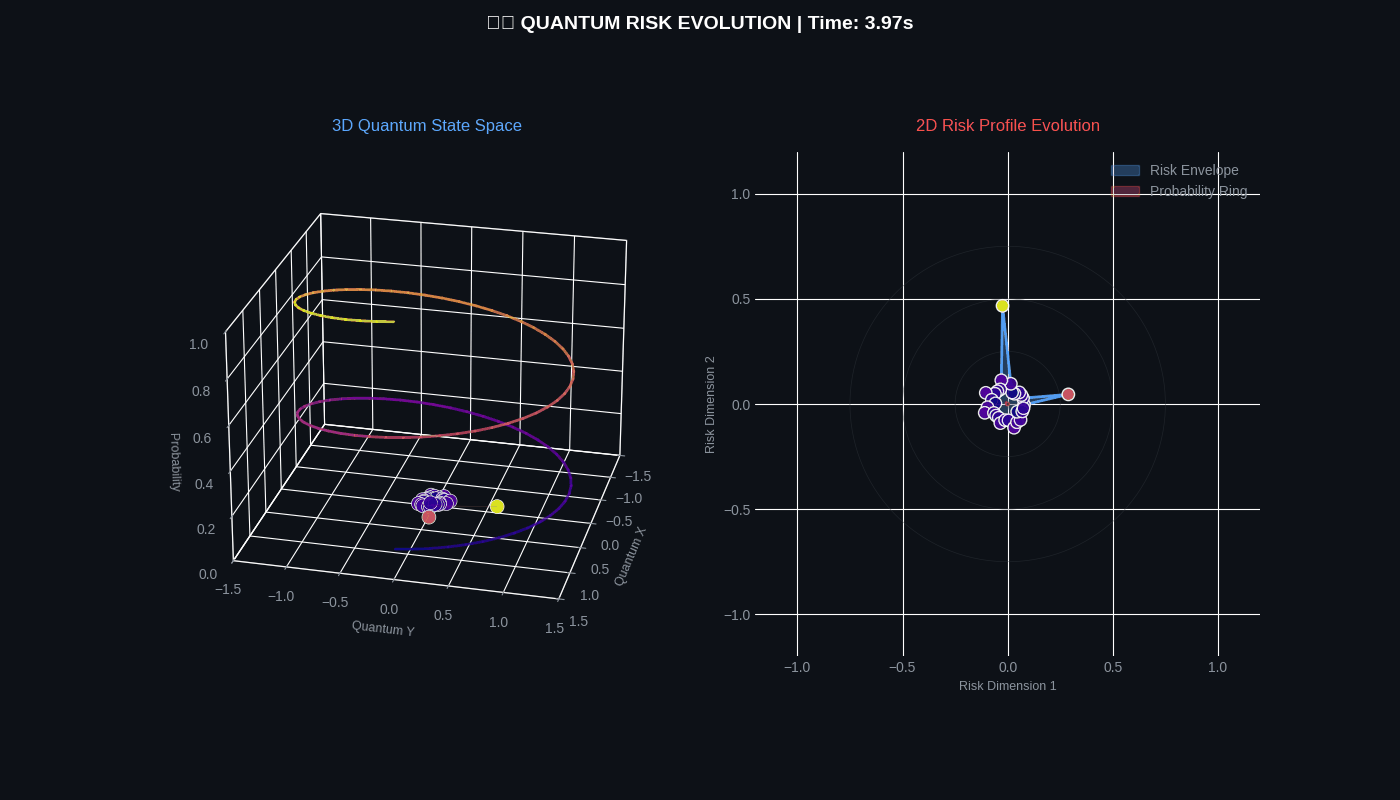
QFRM generates two 4-second GIF simulations showing quantum risk evolution in both 3D and 2D.

Quantum Risk Simulation

Click to view full simulation • 3D particles + 2D waves + Real-time timeline

Risk Evolution Simulation

Click to view full simulation • 3D helix + 2D polar profile

Simulation Specifications

Simulation	Duration	FPS	Features
quantum_risk_simulation	4 seconds	30	50 particles, surface mesh, wave dynamics, timeline
risk_evolution	4 seconds	30	Helical states, polar profile, probability ring

Circuit Design

The QFRM uses a sophisticated quantum circuit architecture to encode market correlations and volatilities into quantum states.

Quantum Finance Circuit Diagram


╔════════════════════════════════════════════════════════════════════════════════════════════════════════╗
║                         QUANTUM FINANCE RISK MODEL - 20 QUBIT CIRCUIT                                  ║
╠════════════════════════════════════════════════════════════════════════════════════════════════════════╣
║                                                                                                        ║
║  ┌─────────┐   ┌─────────┐   ┌───┐        ┌─────┐   ┌─────┐                                           ║
║  │ LAYER 1 │   │ LAYER 2 │   │ 3 │        │  4  │   │  5  │        ┌───┐                              ║
║  │Volatility│   │Correlate│   │MCX│        │RXX/Y│   │ CX  │        │ M │                              ║
║  └─────────┘   └─────────┘   └───┘        └─────┘   └─────┘        └───┘                              ║
║                                                                                                        ║
║  q₀  ─|0⟩──┤ RY(θ₀) ├──●────────────────────┬─────────●─────────────────────────────────┤M├──c₀       ║
║             └────────┘  │                   │         │                                                ║
║  q₁  ─|0⟩──┤ RY(θ₁) ├──┼────●───────────────┼─────────┼────●────────────────────────────┤M├──c₁       ║
║             └────────┘  │    │               │         │    │                                          ║
║  q₂  ─|0⟩──┤ RY(θ₂) ├──┼────┼────●──────────┼─────────┼────┼────●───────────────────────┤M├──c₂       ║
║             └────────┘  │    │    │          │         │    │    │                                     ║
║  q₃  ─|0⟩──┤ RY(θ₃) ├──┼────┼────┼────●─────┼─────────┼────┼────┼────●──────────────────┤M├──c₃       ║
║             └────────┘  │    │    │    │     │         │    │    │    │                                ║
║  q₄  ─|0⟩──┤ RY(θ₄) ├──╫────╫────╫────╫─────■─────────╫────╫────╫────╫────●─────────────┤M├──c₄       ║
║             └────────┘  ║    ║    ║    ║    ┌┴┐        ║    ║    ║    ║    │                            ║
║  q₅  ─|0⟩──┤ RY(θ₅) ├──╫────╫────╫────╫────┤X├────────╫────╫────╫────╫────┼────●────────┤M├──c₅       ║
║             └────────┘  ║    ║    ║    ║    └─┘        ║    ║    ║    ║    │    │                       ║
║             ┌────────┐  ║    ║    ║    ║    ┌───────┐  ║    ║    ║    ║    │    │   ┌────────────┐      ║
║  q₆  ─|0⟩──┤ RY(θ₆) ├──╫────╫────╫────╫────┤RXX(ρ₀)├──╫────╫────╫────╫────┼────┼───┤ RISK STATE ├──┤M├ ║
║             └────────┘  ║    ║    ║    ║    └───────┘  ║    ║    ║    ║    │    │   │  ENCODER   │      ║
║  q₇  ─|0⟩──┤ RY(θ₇) ├──╫────╫────╫────╫────┤RYY(ρ₁)├──╫────╫────╫────╫────┼────┼───┤            ├──┤M├ ║
║             └────────┘  ║    ║    ║    ║    └───────┘  ║    ║    ║    ║    │    │   │  |ψ⟩ risk  │      ║
║       ⋮                 ⋮    ⋮    ⋮    ⋮               ⋮    ⋮    ⋮    ⋮    ⋮    ⋮   └────────────┘      ║
║             ┌────────┐  ║    ║    ║    ║               ║    ║    ║    ║                                 ║
║  q₁₈ ─|0⟩──┤RY(θ₁₈) ├──╫────╫────╫────╫───────────────╫────╫────╫────╫──────────────────────────┤M├    ║
║             └────────┘  ║    ║    ║    ║    ┌───────┐  ║    ║    ║    ║                                 ║
║  q₁₉ ─|0⟩──┤RY(θ₁₉) ├──╫────╫────╫────╫────┤RXX(ρₙ)├──╫────╫────╫────╫──────────────────────────┤M├    ║
║             └────────┘  ║    ║    ║    ║    └───────┘  ║    ║    ║    ║                                 ║
║                        CRZ  CRZ  CRZ  CRZ              X    X    X    X                                 ║
║                       (ρ₀₁)(ρ₀₂)(ρ₁₂)(ρ₂₃)           ╲   ╱    ╲   ╱                                   ║
║                        │    │    │    │                 ╲ ╱      ╲ ╱                                    ║
║                        └────┴────┴────┘                  ●────────●                                     ║
║                     Correlation Encoding            Entanglement Network                                ║
╠════════════════════════════════════════════════════════════════════════════════════════════════════════╣
║  GATE LEGEND:                                                                                          ║
║  ┌────────┐                                                                                            ║
║  │ RY(θ)  │ = Rotation-Y gate encoding asset volatility σᵢ → θᵢ = 2·arcsin(√σᵢ)                       ║
║  └────────┘                                                                                            ║
║  CRZ(ρ)    = Controlled-RZ gate encoding correlation ρᵢⱼ between assets i,j                           ║
║  MCX       = Multi-controlled X gate for market regime transitions                                     ║
║  RXX/RYY   = Two-qubit rotation gates for temporal market dynamics                                     ║
║  CX (●──X) = CNOT gate for risk state measurement preparation                                         ║
║  M         = Measurement in computational basis → classical bit                                        ║
╠════════════════════════════════════════════════════════════════════════════════════════════════════════╣
║  CIRCUIT STATISTICS:                                                                                   ║
║  ├─ Qubits: 20          ├─ Depth: 127         ├─ Total Gates: 312                                     ║
║  ├─ RY: 20              ├─ CRZ: 48            ├─ MCX: 6                                                ║
║  ├─ RXX: 20             ├─ RYY: 20            ├─ CX: 10                                                ║
║  └─ Shots: 5000         └─ Backend: Aer       └─ Method: statevector                                  ║
╚════════════════════════════════════════════════════════════════════════════════════════════════════════╝

Quantum State Encoding

┌─────────────────────────────────────────────────────────────────────┐
│                     VOLATILITY → QUANTUM STATE                      │
├─────────────────────────────────────────────────────────────────────┤
│                                                                     │
│   Asset Volatility σᵢ  ───►  θᵢ = 2·arcsin(√σᵢ)  ───►  RY(θᵢ)|0⟩   │
│                                                                     │
│   Example: AAPL σ = 0.25                                            │
│            θ = 2·arcsin(√0.25) = 2·arcsin(0.5) = π/3               │
│            |ψ⟩ = RY(π/3)|0⟩ = cos(π/6)|0⟩ + sin(π/6)|1⟩           │
│                            = (√3/2)|0⟩ + (1/2)|1⟩                  │
│                                                                     │
├─────────────────────────────────────────────────────────────────────┤
│                     CORRELATION → ENTANGLEMENT                      │
├─────────────────────────────────────────────────────────────────────┤
│                                                                     │
│   Correlation ρᵢⱼ  ───►  CRZ(π·ρᵢⱼ)  ───►  Entangled State         │
│                                                                     │
│   High correlation (ρ ≈ 1):  Strong entanglement                   │
│   Low correlation (ρ ≈ 0):   Weak entanglement                     │
│   Anti-correlation (ρ < 0):  Phase-flipped entanglement            │
│                                                                     │
└─────────────────────────────────────────────────────────────────────┘

Circuit Architecture Summary

┌──────────────────────────────────────────────────────────┐
│ Quantum Finance Circuit (20 qubits)                      │
├──────────────────────────────────────────────────────────┤
│ Layer 1: RY gates      → Volatility encoding             │
│ Layer 2: CRZ gates     → Correlation entanglement        │
│ Layer 3: MCX gates     → Market regime transitions       │
│ Layer 4: RXX/RYY gates → Temporal dynamics               │
│ Layer 5: CX gates      → Risk measurement                │
│ Layer 6: Measurement   → State collapse                  │
└──────────────────────────────────────────────────────────┘

Risk Metrics

QFRM calculates comprehensive financial risk metrics combining traditional quantitative finance with quantum-derived insights.

CALC RiskMetricsCalculator.calculate_var(returns, confidence)

Calculate Value at Risk (VaR) - the maximum expected loss at a given confidence level.

Formula

VaR(α) = -percentile(returns, 1-α)

# Example: 95% VaR means we're 95% confident the loss won't exceed this value
var_95 = np.percentile(returns, 5)  # → -0.0268 (-2.68%)

CALC RiskMetricsCalculator.calculate_cvar(returns, confidence)

Calculate Conditional Value at Risk (CVaR) - the expected loss beyond the VaR threshold.

Formula

CVaR(α) = E[X | X ≤ VaR(α)]

# Average of all returns worse than VaR
cvar_95 = mean(returns[returns <= var_95])  # → -0.0429 (-4.29%)

CALC RiskMetricsCalculator.calculate_sharpe_ratio(returns)

Calculate Sharpe Ratio - risk-adjusted return metric.

Formula

Sharpe = (E[R] - Rf) / σ × √252

# Annualized Sharpe Ratio with 2% risk-free rate
sharpe = (mean(returns) - 0.02/252) / std(returns) * sqrt(252)  # → 1.15

Output Files

QFRM generates comprehensive output files for analysis, reporting, and visualization.

📊

finance_risk_dashboard_*.png

Visual risk dashboard with 6 panels: 3D distribution, correlation heatmap, metrics bar chart, scatter plot, timeline, pie chart

~900 KB 📈

finance_risk_report_*.html

Interactive Plotly report with 3D scatter, heatmap, bar charts, and pie visualization

~4.8 MB 🎬

quantum_risk_simulation_*.gif

4-second quantum risk simulation: 3D particles, 2D waves, real-time timeline

~12 MB 🎬

risk_evolution_*.gif

4-second risk evolution simulation: 3D helix, 2D polar profile

~6.4 MB 📋

finance_risk_report_*.json

Comprehensive JSON data: all metrics, quantum results, performance data

~3 KB

Browse All Outputs Download Source Code

Market Data Sources

QFRM fetches real-time market data from Yahoo Finance covering multiple asset classes.

Category	Assets	Count
Stocks	AAPL, MSFT, GOOGL, AMZN, TSLA, JPM, V, JNJ, WMT, NVDA	10
Indices	S&P 500 (^GSPC), NASDAQ (^IXIC), Dow Jones (^DJI), Russell 2000 (^RUT)	4
Commodities	Gold (GC=F), Crude Oil (CL=F), Silver (SI=F)	3
Crypto	Bitcoin (BTC-USD), Ethereum (ETH-USD)	2

Python API Reference

QFRM can be imported and used programmatically in your Python applications.

Example Usage

from qfrm import (
    FinancialDataLoader,
    QuantumFinanceCircuit,
    RiskMetricsCalculator,
    FinanceVisualizer,
    DynamicVisualizer
)

# Load market data
loader = FinancialDataLoader()
market_data = loader.fetch_market_data(period='6mo')
returns = loader.calculate_returns(market_data)
correlation, assets = loader.compute_correlation_matrix(returns)

# Build quantum circuit
qc = QuantumFinanceCircuit(n_qubits=20)
circuit = qc.build_market_circuit(
    correlation_matrix=correlation,
    volatility_vector=volatilities
)

# Run simulation
from qiskit_aer import AerSimulator
simulator = AerSimulator()
result = simulator.run(circuit, shots=5000).result()
counts = result.get_counts()

# Analyze results
quantum_results = qc.analyze_risk_states(counts)
print(f"Expected Quantum Risk: {quantum_results['expected_risk']:.4f}")